实数的分类,实数是什么意思,实数的概念是什么。有理数的分类是什么?一、实数的分类实数可分为有理数和无理数,或代数数和超越数,实数的具体分类整数、有限小数、无限小数是实数和(2)0和正数,负数是实数,所有实数是什么意思?有理数和无理数统称为实数。
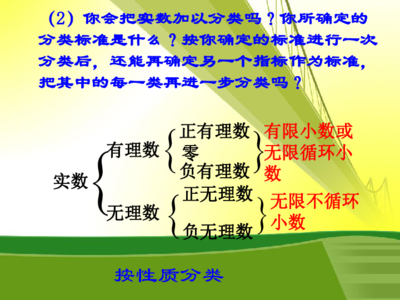
1、实数的运算种类是哪六种
实数的运算类型有:加、减、乘、除、幂、根。1.加法是将两个以上的数组合成一个数,其结果称为和。2.减法是用一个量减去另一个量的运算,结果叫做差。3.乘法是指将相同的数相加的捷径,其结果称为积。4.除法是求两个因子和其中一个因子的乘积求另一个因子的运算,结果叫做商。5.幂是同一个数或世代数乘以自身若干次的运算,其结果称为幂。

2、全体实数是什么意思
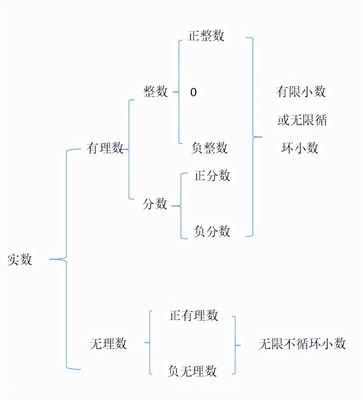
所有实数指所有实数,有理数和无理数统称为实数。实数如果按有理数和无理数分类,有实数、有理数、正有理数、零、负有理数、有限小数或无限循环小数无理数、正无理数、负无理数和无限循环小数。所有实数是什么意思?有理数和无理数统称为实数。实数的分类方法有以下几种:按有理数和无理数分类,有实数、有理数、正有理数、零、负有理数、有限小数或无限循环小数无理数、正无理数、负无理数和无限循环小数。由于有理数和无理数都有正数和负数之分,所以实数可以根据正负概念分为实数、正实数和正实数。
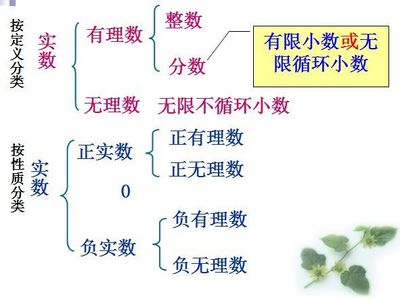
3、有理数有几种分类,分别是什么
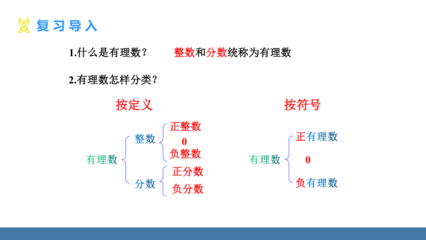
有理数通常有两种分类方法。有理数分为整数和分数整数分为正整数,0,负整数分数分为正分数和负分数两种。有理数分为正有理数,0和负有理数分为正整数,正分数负有理数分为负整数,负分数备注:有限小数和无限循环小数都属于分数。有理数的分类是什么?有理数有两种分类,分别是:(1)根据有理数的定义分类;(2)根据有理数的性质分类。
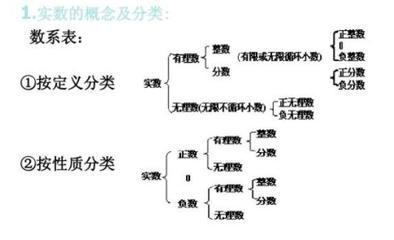
数学上,有理数是整数a与正整数b的比值,比如3/8,一般规律是a/b,0也是有理数。有理数是整数和分数的集合,整数也可以看作分母为1的分数。有理数的小数部分是一个有限或无限循环数。不是有理数的实数称为无理数,即无理数的小数部分是无限循环数。扩展数据:加法运算1。将两个符号相同的数字相加,以相同的符号作为加数,然后将绝对值相加。
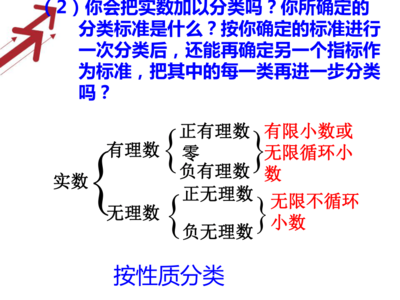
4、实数的具体分类
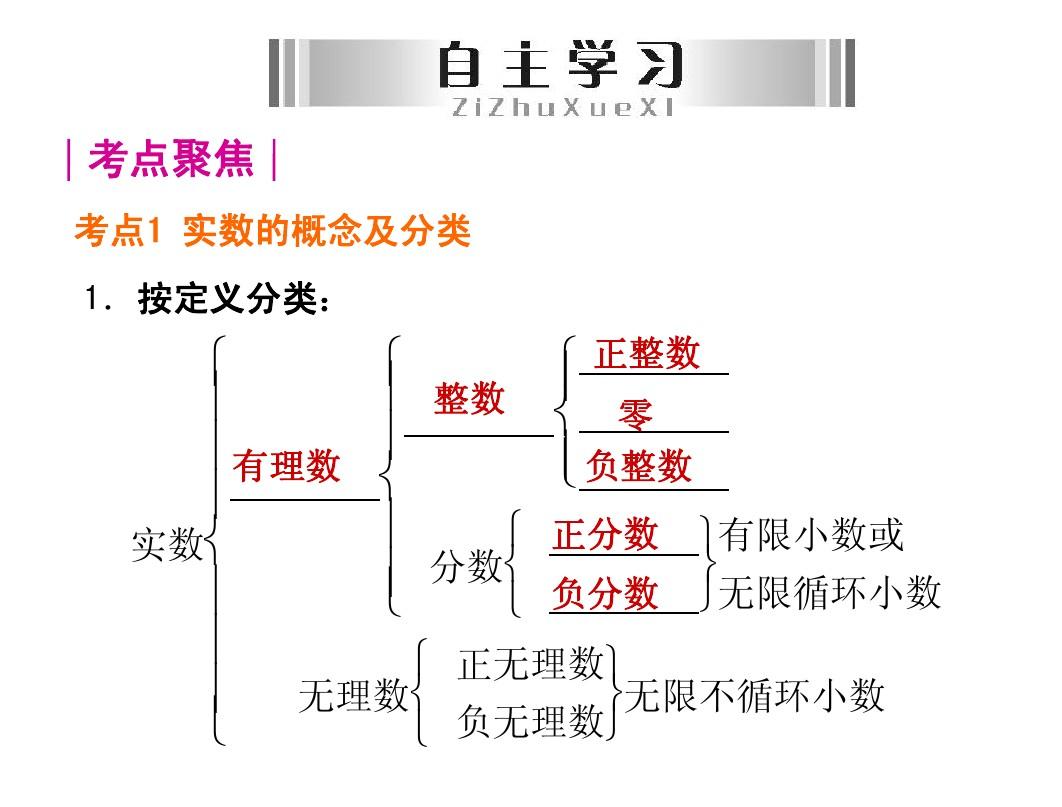
整数,有限小数,无限小数是实数和(2)0和正数,负数是实数。1)可分为整数,分数整数可分为正整数,负整数分数可分为正分数,负分数可分为正分数,负正分数可分为正整数,负分数可分为负整数和负分数。实数有理数,无理数有理数正数和负数无理数无限循环小数。(1)实数可分为整数和分数,整数可分为正整数、0和负整数。
5、实数是指什么
实数是什么概念?有理数和无理数统称为实数。每一个实数都可以用数轴上的一个点来表示;相反,数轴上的每个点都代表一个实数。实数有两种分类。一、分类是:正数、负数、0;另一种分类是:有理数和无理数。实数指有理数和无理数。数学上,实数定义为数轴上对应点的数。实数可以直观地看作是有限小数和无限小数、实数和数轴上的点一一对应。
实数和虚数一起构成一个复数。实数可分为有理数和无理数,或代数数和超越数。实数集通常用黑色字母R表示,R代表n维实数空间。实数是不可数的。实数是实数理论的核心研究对象。发展历史:公元前500年左右,以毕达哥拉斯为首的希腊数学家认识到有理数不能满足几何中的需要,但毕达哥拉斯本人并不承认无理数的存在。直到17世纪,实数才在欧洲被广泛接受。
6、实数的分类,实数可以分为几类?
实数可以分为两类,分别指哪两类?不清楚的考生赶紧看看。我精心准备了“实数的分类。实数可以分为多少种类型?”,持续关注本站会持续获取更多考试信息!实数的分类,实数可以分为多少类?一、实数的分类实数可分为有理数和无理数,或代数数和超越数。实数集通常用黑色字母R表示,R代表n维实数空间。实数是不可数的。
所有实数的集合可以称为实数系或实数连续统。任何完整的阿基米德有序域都可以称为实数系。在保序同构的意义上是唯一的,常以R表示,由于R是定义算术运算的算术系统,所以有实数系之称。实数可以用来度量连续的量。理论上,任何实数都可以表示为一个无限小数,小数点右边是一个无穷级数(循环或非循环)。
7、什么是实数
实数是有理数和无理数的总称,包括0。数学上,实数定义为数轴上对应点的数,实数可以直观地看作是有限小数和无限小数、实数和数轴上的点一一对应。实数能实现的基本运算有加、减、乘、除、乘等,对于非负数(即正数和0),也可以进行开方运算。实数加、减、乘、除(除数不为零)和平方的结果仍然是实数,任何实数都可以被提升到奇数次幂,结果仍然是一个实数。只有非负实数才能被提升到偶次幂,结果仍然是实数。
